https://www.acmicpc.net/problem/23291
23291번: 어항 정리
마법사 상어는 그동안 배운 마법을 이용해 어항을 정리하려고 한다. 어항은 정육면체 모양이고, 한 변의 길이는 모두 1이다. 상어가 가지고 있는 어항은 N개이고, 가장 처음에 어항은 일렬로 바
www.acmicpc.net
문제
마법사 상어는 그동안 배운 마법을 이용해 어항을 정리하려고 한다. 어항은 정육면체 모양이고, 한 변의 길이는 모두 1이다. 상어가 가지고 있는 어항은 N개이고, 가장 처음에 어항은 일렬로 바닥 위에 놓여져 있다. 어항에는 물고기가 한 마리 이상 들어있다. <그림 1>은 어항 8개가 바닥 위에 놓여있는 상태이며, 칸에 적힌 값은 그 어항에 들어있는 물고기의 수이다. 편의상 어항은 정사각형으로 표현했다.

<그림 1>
어항을 한 번 정리하는 과정은 다음과 같이 이루어져 있다.
먼저, 물고기의 수가 가장 적은 어항에 물고기를 한 마리 넣는다. 만약, 그러한 어항이 여러개라면 물고기의 수가 최소인 어항 모두에 한 마리씩 넣는다. 위의 예시의 경우 물고기의 수가 가장 적은 어항에는 물고기가 2마리 있고, 그러한 어항은 2개가 있다. 따라서, 2개의 어항에 물고기를 한 마리씩 넣어 <그림 2>와 같아진다.

<그림 2>
이제 어항을 쌓는다. 먼저, 가장 왼쪽에 있는 어항을 그 어항의 오른쪽에 있는 어항의 위에 올려 놓아 <그림 3>이 된다.
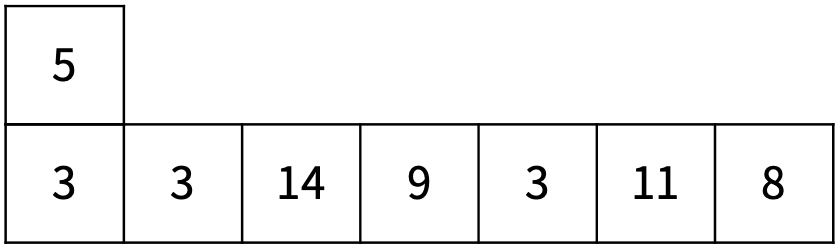
<그림 3>
이제, 2개 이상 쌓여있는 어항을 모두 공중 부양시킨 다음, 전체를 시계방향으로 90도 회전시킨다. 이후 공중 부양시킨 어항을 바닥에 있는 어항의 위에 올려놓는다. 바닥의 가장 왼쪽에 있는 어항 위에 공중 부양시킨 어항 중 가장 왼쪽에 있는 어항이 있어야 한다. 이 작업은 공중 부양시킨 어항 중 가장 오른쪽에 있는 어항의 아래에 바닥에 있는 어항이 있을때까지 반복한다.
먼저, <그림 4>와 같이 어항이 놓인 상태가 변하고, 한 번 더 변해서 <그림 5>가 된다.
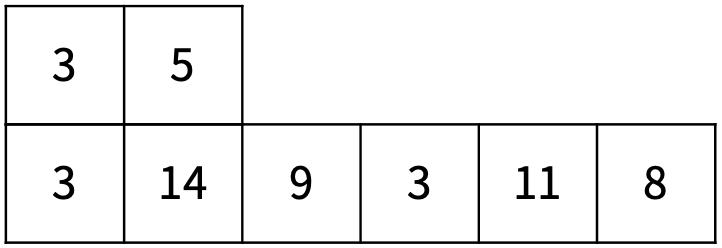
<그림 4>
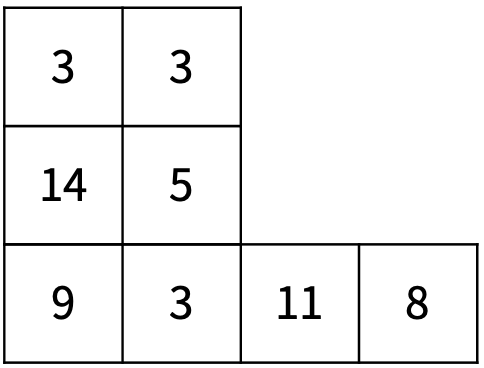
<그림 5>
<그림 5>에서 한 번 더 어항을 공중 부양시키는 것은 불가능하다. 그 이유는 <그림 6>과 같이 공중 부양시킨 어항 중 가장 오른쪽에 있는 어항의 아래에 바닥에 있는 어항이 없기 때문이다.
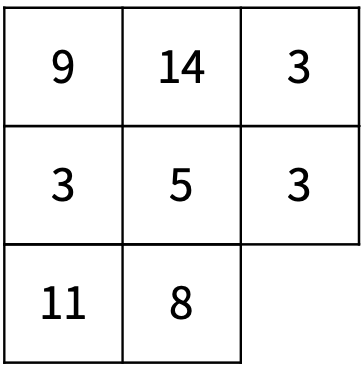
<그림 6>
공중 부양 작업이 모두 끝나면, 어항에 있는 물고기의 수를 조절한다.
모든 인접한 두 어항에 대해서, 물고기 수의 차이를 구한다. 이 차이를 5로 나눈 몫을 d라고 하자. d가 0보다 크면, 두 어항 중 물고기의 수가 많은 곳에 있는 물고기 d 마리를 적은 곳에 있는 곳으로 보낸다. 이 과정은 모든 인접한 칸에 대해서 동시에 발생한다. 이 과정이 완료되면 <그림 7>이 된다.
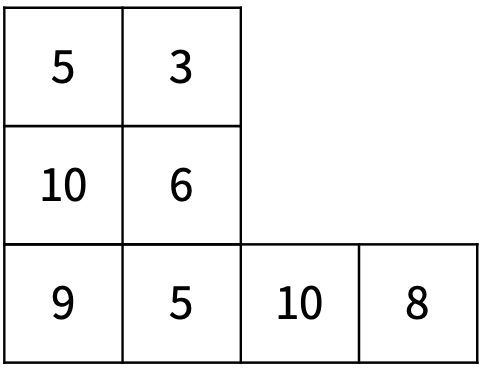
<그림 7>
이제 다시 어항을 바닥에 일렬로 놓아야 한다. 가장 왼쪽에 있는 어항부터, 그리고 아래에 있는 어항부터 가장 위에 있는 어항까지 순서대로 바닥에 놓아야 한다. <그림 8>이 바닥에 다시 일렬로 놓은 상태이다.

<그림 8>
다시 공중 부양 작업을 해야 한다. 이번에는 가운데를 중심으로 왼쪽 N/2개를 공중 부양시켜 전체를 시계 방향으로 180도 회전 시킨 다음, 오른쪽 N/2개의 위에 놓아야 한다. 이 작업은 두 번 반복해야한다. 두 번 반복하면 바닥에 있는 어항의 수는 N/4개가 된다. <그림 9>는 이 작업을 1번 했을 때, <그림 10>은 다시 한 번 더 했을 때이다.
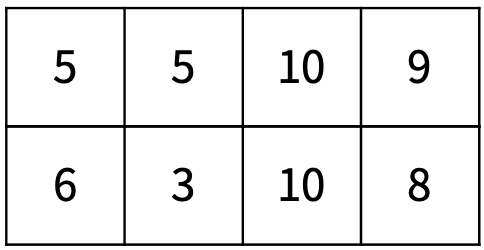
<그림 9>
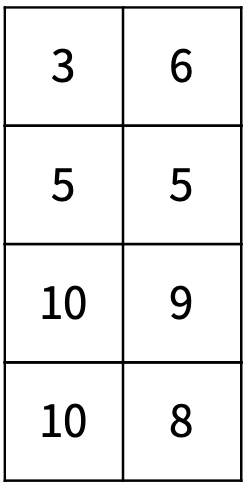
<그림 10>
여기서 다시 위에서 한 물고기 조절 작업을 수행하고, 바닥에 일렬로 놓는 작업을 수행한다. <그림 10>에서 조절 작업을 마친 결과는 <그림 11>이 되고, 여기서 다시 바닥에 일렬로 놓는 작업을 수행하면 <그림 12>가 된다.

<그림 11>

<그림 12>
어항의 수 N, 각 어항에 들어있는 물고기의 수가 주어진다. 물고기가 가장 많이 들어있는 어항과 가장 적게 들어있는 어항의 물고기 수 차이가 K 이하가 되려면 어항을 몇 번 정리해야하는지 구해보자.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int N, K;
int bsize = 2;
int answer = 0;
vector<int> bowl;
int add() {
int min = 10001;
vector<int> mv;
for (int b = 0; b < bowl.size(); b++) {
if (min == bowl[b])
mv.push_back(b);
else if (min > bowl[b]) {
min = bowl[b];
mv.clear();
mv.push_back(b);
}
else continue;
}
for (int a = 0; a < mv.size(); a++)
bowl[mv[a]]++;
return 0;
}
vector<vector<int>> turnv(vector<vector<int>> oldv, bool e) {
int n = oldv.size();
if (!e) {
if (oldv.size() > oldv.front().size()) {
vector<vector<int>> newv(oldv.front().size(), vector<int>(n, 0));
for (int y = 0; y < oldv.front().size(); y++) {
for (int x = 0; x < n; x++) {
newv[y][x] = oldv[x][oldv.front().size() - 1 - y];
}
}
return newv;
}
else {
n = oldv.front().size();
vector<vector<int>> newv(n, vector<int>(oldv.size(), 0));
for (int y = 0; y < n; y++) {
for (int x = 0; x < oldv.size(); x++) {
newv[y][x] = oldv[x][n - 1 - y];
}
}
return newv;
}
}
else {
vector<vector<int>> newv(n, vector<int>(n, 0));
for (int y = 0; y < n; y++) {
for (int x = 0; x < n; x++) {
newv[y][x] = oldv[x][n - 1 - y];
}
}
return newv;
}
}
vector<vector<int>> regulate(vector<vector<int>> bottom) {
vector<vector<int>> ret = bottom;
int x[] = { -1,1,0,0 };
int y[] = { 0,0,-1,1 };
for (int i = 0; i < bottom.size(); i++) {
for (int j = 0; j < bottom[i].size(); j++) {
for (int k = 0; k < 4; k++) {
int by = i + y[k], bx = j + x[k];
if (by >= bottom.size() || by < 0 || bx >= bottom[i].size() || bx < 0) continue;
else if (bx >= bottom[by].size()) continue;
int diff = bottom[i][j] - bottom[by][bx];
if (diff > 0) {
ret[i][j] -= diff / 5;
ret[by][bx] += diff / 5;
}
}
}
}
return ret;
}
vector<int> line(vector<vector<int>> bottom, int b_size, bool flag) {
vector<int> ret;
if (flag) {
if (b_size == bottom.front().size()) {
for (int j = 0; j < b_size; j++) {
for (int i = 0; i < b_size; i++) {
ret.push_back(bottom[i][j]);
}
}
}
else {
for (int j = 0; j < b_size - 1; j++) {
for (int i = 0; i < b_size; i++) {
ret.push_back(bottom[i][j]);
}
}
for (int k = b_size - 1; k < bottom[0].size(); k++) ret.push_back(bottom[0][k]);
}
}
else {
for (int j = 0; j < b_size; j++) {
for (int i = 0; i < 4; i++) {
ret.push_back(bottom[i][j]);
}
}
}
return ret;
}
vector<vector<int>> divided() {
vector<vector<int>> tmp(2, vector<int>(N / 2, 0));
for (int i = 0; i < N / 2; i++) {
tmp[1][i] = bowl[N / 2 - i - 1];
tmp[0][i] = bowl[N / 2 + i];
}
vector<vector<int>> toturn(2, vector<int>(N / 4, 0));
for (int y = 0; y < 2; y++)
for (int x = 0; x < N / 4; x++)
toturn[y][x] = tmp[y][x];
vector<vector<int>> ret1(N / 4, vector<int>(2, 0));
vector<vector<int>> ret(2, vector<int>(N / 4, 0));
if (2 == N / 4) ret1 = turnv(toturn, true);
else ret1 = turnv(toturn, false);
if (2 == N / 4) ret = turnv(ret1, true);
else ret = turnv(ret1, false);
for (int i = 0; i < 2; i++) tmp[i].erase(tmp[i].begin(), tmp[i].begin() + (N / 4));
for (int t = 0; t < ret.size(); t++)tmp.push_back(ret[t]);
return tmp;
}
int main() {
cin >> N >> K;
for (int i = 0; i < N; i++) {
int tmp;
cin >> tmp;
bowl.push_back(tmp);
}
while (1) {
add();
vector<vector<int>> bottom;
vector<int> top;
top.push_back(bowl[0]);
bowl.erase(bowl.begin() + 0);
bottom.push_back(bowl);
bottom.push_back(top);
int test = 2;
int bowl_size = 2;
bool equil = false; // true : n*n
while (bottom[0].size() - (bowl_size - 1) >= bowl_size) {
if (!equil) {
vector<vector<int>> toturn(bowl_size, vector<int>(bowl_size - 1, 0));
vector<vector<int>> turnned(bowl_size - 1, vector<int>(bowl_size, 0));
for (int y = 0; y < bowl_size; y++) {
for (int x = 0; x < bowl_size - 1; x++) {
toturn[y][x] = bottom[y][x];
}
}
turnned = turnv(toturn, equil);
equil = true;
bottom[0].erase(bottom[0].begin(), bottom[0].begin() + (bowl_size - 1));
for (int er = 1; er < bowl_size; er++) bottom.pop_back();
for (int t = 0; t < turnned.size(); t++)bottom.push_back(turnned[t]);
}
else if (equil) {
vector<vector<int>> toturn(bowl_size, vector<int>(bowl_size, 0));
vector<vector<int>> turnned(bowl_size, vector<int>(bowl_size, 0));
for (int y = 0; y < bowl_size; y++) {
for (int x = 0; x < bowl_size; x++) {
toturn[y][x] = bottom[y][x];
}
}
turnned = turnv(toturn, equil);
bottom[0].erase(bottom[0].begin(), bottom[0].begin() + bowl_size);
for (int er = 1; er < bowl_size; er++) bottom.pop_back();
for (int t = 0; t < turnned.size(); t++)bottom.push_back(turnned[t]);
equil = false;
bowl_size++;
}
}
bottom = regulate(bottom);
bowl = line(bottom, bowl_size, true);
bottom = divided();
bottom = regulate(bottom);
bowl = line(bottom, N / 4, false);
answer++;
int max = max_element(bowl.begin(), bowl.end()) - bowl.begin();
int min = min_element(bowl.begin(), bowl.end()) - bowl.begin();
if (bowl[max] - bowl[min] <= K) break;
}
cout << answer << endl;
return 0;
}'Coding Test' 카테고리의 다른 글
| [백준]14503 로봇청소기 (0) | 2023.04.08 |
|---|---|
| [백준]2961 도영이가 만든 맛있는 음식 (0) | 2023.04.08 |
| [백준]17837 새로운 게임2 (0) | 2022.04.28 |
| [백준]20055 컨베이어 벨트 위의 로봇(57%시간초과) (0) | 2022.04.26 |
| [백준]23289 온풍기 안녕! (실패) (0) | 2022.04.26 |